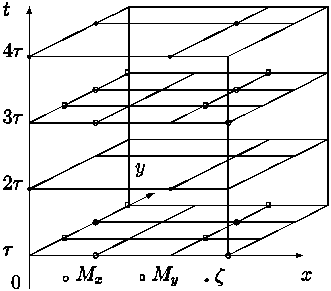
Figure 1. The H - N numerical grid in the x - y - t space
Andrzej Jankowski
Institute of Oceanology of PAS
Sopot, Poland
e-mail: jankowsk@iopan.gda.pl
Key words: Baltic sea, barotropic numerical model, wind - driven circulation
1. Introduction
The results of the application of a barotropic numerical model to estimate wind - driven circulation in o the Baltic Sea are described. The non - linear version of the model was adapted to investigate the seiches characteristics in small and shallow water basin (Frischmuth and Jankowski, 1996). The linear baroclinic version of the model was applied in diagnostical studies of mean climatic water circulation in the Baltic Sea (e.g. Jankowski and Kowalik, 1980; Jankowski, 1983; 1996).
The results of the computations are shown in a form of charts of stream function for mass transport and sea level as well as of vectors of the mean - depth and the surface currents.
2 Model description
2.1 Equations and boundary conditions
Model is based on following equations of motion and continuity equation
(Ramming and Kowalik, 1980; Simons, 1973):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
Integration of the hydrostatic equation (3) with respect to z and taking into account boundary conditions (6) for pressure yields:
| (11) |
Differentiating (11) with respect to x and y and substituting the results into eqs. (1) - (2) we obtain:
| |||||||||||||||||||
| |||||||||||||||||||
2.2 Mass transport and sea level equations
Integrating eqs. (14) - (15) and continuity equation (4) with respect to z from z = - H to z = z and taking into account boundary conditions (7) - (10) we obtain the equations to calculate the mass transport components and sea level:
| (14) |
| (15) |
| (16) |
|
Pertinent lateral boundary and initial conditions for the mass transport and sea level equations (14) - (16) can be written in a form (Ramming and Kowalik, 1980; Jankowski, 1988):
| (17) |
| (18) |
| (19) |
Marchuk and Kagan (1977) proved that the set of eqs. (14) - (16) subject to the boundary (17), (18) and initial (19) conditions, possesses a unique solution; therefore after estimation the external forces and model parameters the set of equations (14) - (16) can be integrated through time to seek out the values of the mass transport components Mx, My and z in the sea basin area.
2.3 Equation for the horizontal components of the current velocity
For case of stationary atmospheric forcing and disregarding the lateral friction terms in the equations of motion (12) - (13) it can be easy to estimate horizontal currents velocity components. With the above mentioned assumptions eqs. (12), (13) can be rewritten in the form:
| |||||||||||||
| |||||||||||||
Assuming that the atmospheric pressure, wind stress components the values of sea level z and mass transport components Mx, My (from the solution of the set of eqs. (14) - (16) ) are known the set of eqs. (20), (21) resolve into an equation for complex velocity D = u + i v (Jankowski, 1988; Ramming and Kowalik, 1980):
| (22) |
| (23) |
| |||||||||||||||
| |||||||||||||||
In the case of constant with z the vertical eddy viscosity coefficient Kz, an analytical, Ekman - type, solution of eq. (22) with boundary conditions (25), (26) may be found out in the form (Jankowski, 1988):
| ||||||||||||||||||||||||||||||||||
| (27) |
Introducing into (27) the values of sea level z and mass transport components Mx, My from the solution of the set of eqs. (14) - (16) and estimates of model parameters: i.e. the components of tangential wind stress tsx, tsy and bottom stress tbx, tby, and the vertical eddy viscosity coefficient Kz one can calculate the horizontal components of the current velocity vector.
2.4 Model parameters and atmospheric forcing
Tangential wind stress components tsx,
tsy and tangential bottom water stress components tbx,
tby were calculated by well tested formulae used in hydrodynamical -
numerical models (Simons, 1973; Ramming and Kowalik, 1980;
Kowalik and Murty, 1993; Jankowski, 1988):
- wind stress components:
| (28) |
| (29) |
In our calculations the standard values for air density ra = 1.3 ·10-3g/cm3, for drag coefficient CD = 2.6·10-3 and for the bottom friction coefficient r = 2.5 ·10-3, usually used in numerical calculations of storm surges and water circulation in the natural basins (Simons, 1973; Ramming and Kowalik, 1980), were applied.
For the case of mean climatic, multi - year averaged atmospheric forcing, first the geostrophic wind was determined from the distribution of atmospheric pressure:
| (30) |
Next wind stress components are estimated by standard formulas (29) mentioned above with Wa = Wags and taking into account deflection angle between the geostrophic surface wind Wags and "real" surface wind Wa a equal to 15o (in counterclockwise direction) (Jankowski, 1988; Svansson, 1972).
The eddy viscosity coefficient Kz was estimated by the Felsenbaum's theory of wind - driven currents, in which values of Kz, depended on wind velocity, Coriolis parameter and basin depth can be estimated by expressions (Ramming and Kowalik, 1980; Jankowski, 1988; Svansson, 1972):
| |||||||||||
The coefficient of the lateral eddy viscosity (the lateral friction coefficient) Ah as it is been found out (cf. Defant, 1961; Ozmidov, 1968) is dependent on spatial scale of the dynamic processes and in general satisfies the Richardson law:
| (32) |
In shallow water basin the influence (role) of the lateral friction from physical point of view is minor comparing to bottom friction, but because of bottom variability and irregularity of the shore line one can include the lateral friction terms into numerical model treate them as smoothing terms, to filter out the parasite instabilties generated during numerical computations due to above mentioned variabilities of the bottom relief and coast line.
In the model calculations the lateral eddy viscosity was estimated by formula (33) with the horizontal scale L equal to several space steps of numerical grid. After some experiments the final computations were carried out with the value of the lateral coefficient of order of Ah (5 ·107 cm2/s).
3. Numerical method of solution of mass transport and sea level equations
The finite explicite difference scheme used by Hansen (Hansen, 1962: Ramming and Kowalik, 1980) was applied to the system of eqs. (14) -(16), and the numerical calculations were carried out with time step equal to 60 seconds and space steps equal to hx = hy = h = 5 Nm. The locations of the calculated variables on the finite difference grid (Arakawa C - grid) are depicted in Fig. 1 and the layout of numerical grid points in xy - plane are shown in Fig. 2.
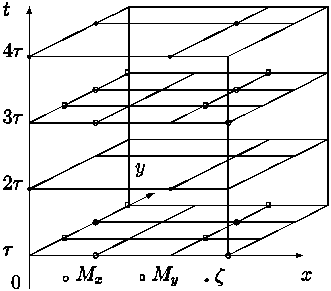
Figure 1. The H - N numerical grid in the x - y - t space
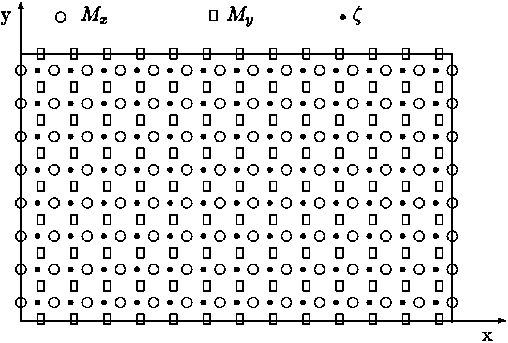
Figure 2. The H - N numerical grid in the x - y plane
Finite difference form of equations
for mass transport and sea level (14) - (16)
is as follows
(Ramming and Kowalik, 1980; Kowalik and Murty, 1993):
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| (35) |
| (36) |
| (37) |
| |||||||
| |||||||
| ||||||||||||
| ||||||||||||
| (42) |
Results and comments
The model set up on the cartesian square numerical grid covering the Baltic Sea area on the sea map in the Mercator projection (basic coordinate lines: 19o E and 60o N, respectively).
Bottom topography of the Baltic Sea for the numerical model was smoothed and Fig. 3 shows final form of the bottom relief of the sea basin used in the model computations.
In Fig. 4 the calculated wind velocity vectors fields for selected months are presented as well as the multi - year atmospheric surface pressure.
Figs. 5 - 8 display distributions of stream function for mass transport, sea level, mean - depth currents and suface currents for the selected months calculated by the model.
Figs. 9 - 12 present results of calculations of stream function for mass transport, sea level, mean - depth currents and surface currents for the case of strong winds of constant velocity equal to 10 m/s blowing from basic wind directions.
Stream function Y was calculated from the mass transport components Mx, My by means of the steady - state form of sea level equation (16) and the standard formulas:
| |||||||||
The spatial distributions of the circulational characteristics for the mean, multi - year averaged, wind fields for selected months (Figs. 5 - 8) as well as for strong wind (Figs. 9 - 12) are well correlated with the atmospheric forcing and the Baltic Sea morphometry. The basics features of circulation - cyclonic and anticyclonic gyres are located in the regions of the Baltic Sea with the specific bottom relief and shore line structures (deeps, furrows and banks, bays etc.).
The estimated wind - driven circulation patterns show the essential influence of the bottom relief and the complex coast lines of the basin on the calculated circulational characteristics and they confirm the results of the other investigaters (e.g. Kowalik and Staskiewicz, 1976; Simons, 1978; Kielmann, 1981; Mälkki and Tamsalu, 1975; Krauss and Brügge, 1991).
Water circulation in the Baltic Sea, which is controlled by the complex coast lines and bottom relief and driven by the wind and the thermohaline forcing (the last not considered in the presented calculations), may have some influence on the distributions of ecological, biological or pollution fields.
Presented patterns of the wind - driven circulation in the barotropic Baltic Sea may serve as the hydrological background for understanding of variability of the ecological parameters giving the overall picture of sea water dynamics in barotropic case.
References
Defant A.I., 1961, Physical oceanography, vol. 1, Pergamon Press, Oxford,
London, Paris, New York, 729 pp.
Frischmuth K., Jankowski A., 1996, Estimation of period of free oscillations
(seiches) in the Kirrbucht. Oceanologia, No. 38 (4), 503 - 526,
Garbalewski C., Malicki J., 1971, Influence of thermal stratification of the
lower atmosphere and water temperature on wind velocity above
the Baltic. Wiadomosci Sluzby Hydrol. i Meteorol., 7 (19),
37-46 (in Polish)
Hansen W., 1962, Hydrodynamical methods applied to oceanographic
problems. Proc.Sympos. Mathem. - Hydrodyn. Methods of Phys.
Oceanography, Hamburg, 25 - 34
Jankowski A., 1983b, An model H-N for the calculation of wind - and density
- driven circulation in the Baltic Sea. Part II. Density - driven
circulation in the summer season. Oceanologia, No. 16, 17-40
Jankowski A., 1988, Mathematical modelling of water circulation in
the Baltic Sea. Seria "Prace habilitacyjne", Ossolineum, Wroc/law 1988,
1 - 281 (in Polish)
Jankowski A., 1996, Vertical water circulation in the southern Baltic Sea
and its environmental implications., Oceanologia,
No. 38 (4), 483 - 501,
Jankowski A., Kowalik Z., 1980, Diagnostic model of wind - and density -
driven currents in the Baltic Sea. Oceanologica Acta, vol. 3, No. 3, 301-308
Kielmann J., 1981, Grundlagen und Anwendung eines numerischen Modells
der geschichen Ostsee., Ber. Inst. Meereskunde Universität Kiel, 87a, b
Kowalik Z., Murty T.S., 1993, Numerical modeling of ocean dynamics,
Advanced Series on Ocean Engineering - Vol. 5, World Scientific,
Singapore - New Jersey - London - Hong Kong, 1993, 481 pp.
Kowalik Z., Staskiewicz A., 1976,
Diagnostic model of the circulation in
the Baltic Sea., Dt. hydrogr. Z., 29, No. 6, 239 - 250
Marchuk G.I., Kagan B.A., 1977, Ocean tides. Gidrometeoizdat, Leningrad,
296 pp. (in Russian)
Mälkki P., Tamsalu R., 1985 Physical features of the Baltic Sea. Finnish
Marine Research, 252, 109pp.
Ozmidov R.V., 1968, Horizontal turbulence and turbulent exchange in
the ocean , Isdat. Nauka, Moskva, 200 pp. (in Russian)
Ramming H.G., Kowalik Z., 1980, Numerical modelling of marine
hydrodynamics. Elsevier Oceanography Series, 26, 1980, 369 pp.
Simons T.J., 1973, Development of three - dimensional numerical models
of the Great Lakes, Inland Water Directoriate Scientific Series No. 12,
Canada Centre for Inland Waters, Burlington, Ontario, 1973, 26 pp.
Simons T.S., 1978, Wind - driven circulations in the southwest Baltic.
Tellus, 30, 272 - 283
Svansson A., 1972, Canal models of sea level and salinity variations in
the Baltic and adjacent waters., Series Hydrography, Rap. No. 26,
Fishery Board of Sweden, 72 pp.
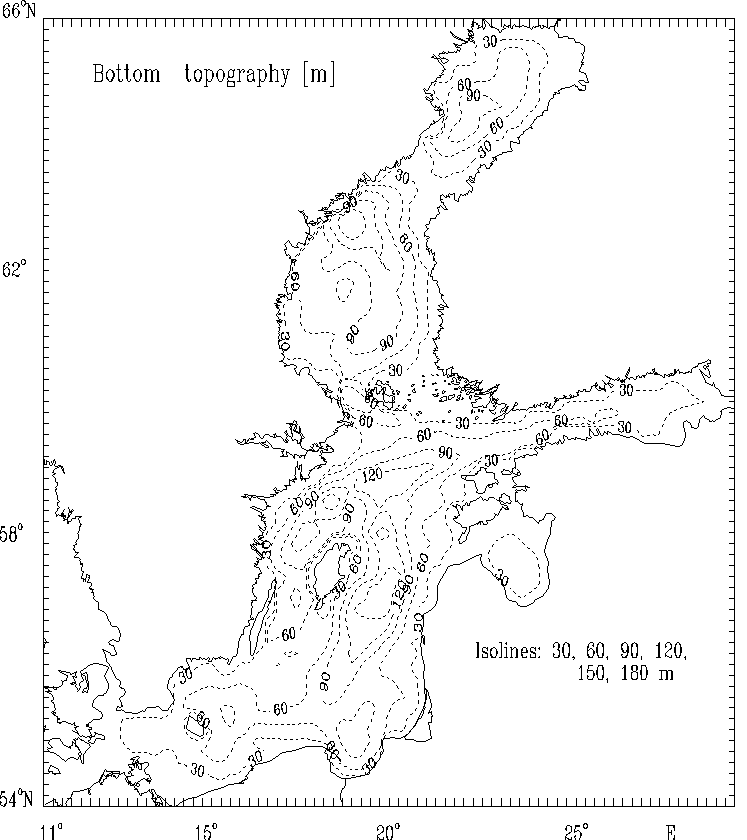
Figure 3. Bottom topography [ m ] of the Baltic Sea used in the model
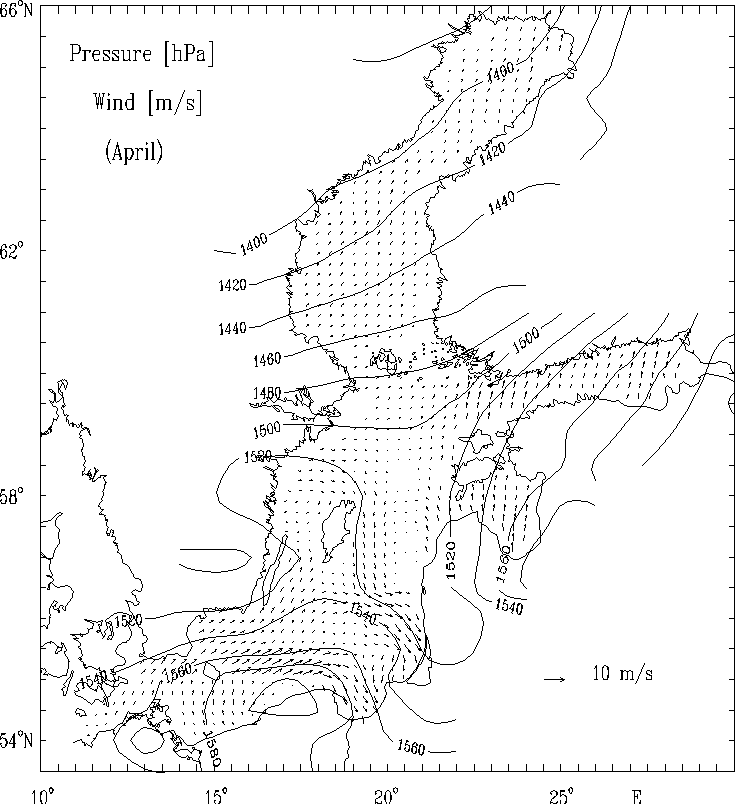
Figure 4a. The multi-year averaged surface atmospheric pressure anomaly [hPa]
and the calculated quasi-geostrophic wind field [m/s] for selected months:
April
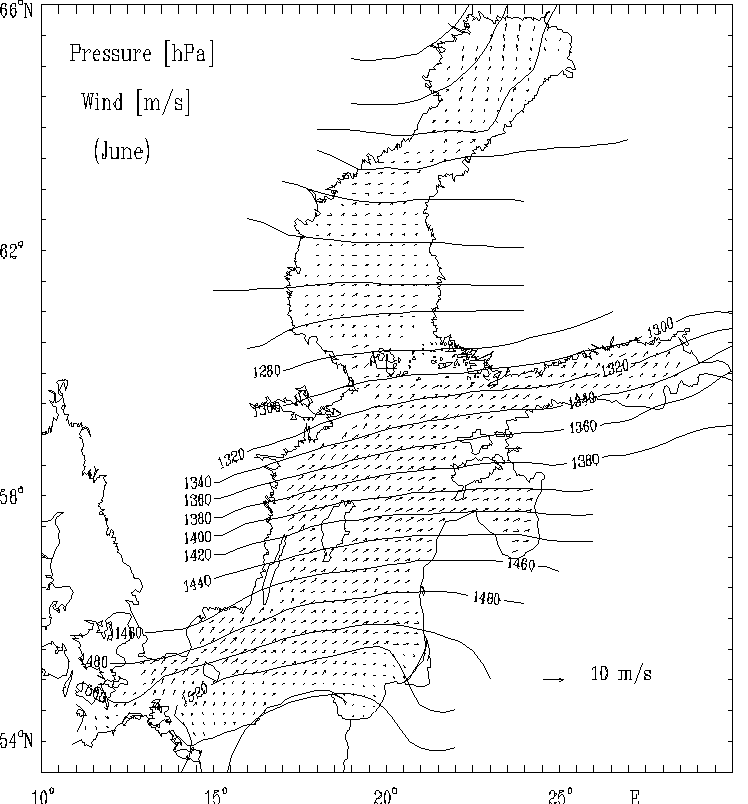
Figure 4b. The multi-year averaged surface atmospheric pressure anomaly [hPa]
and the calculated quasi-geostrophic wind field [m/s] for selected months:
June
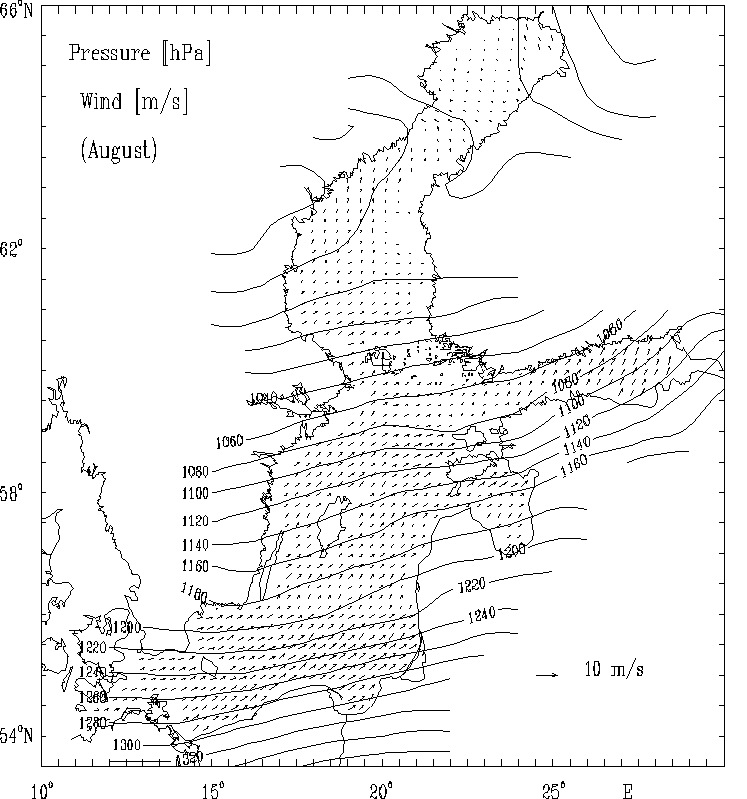
Figure 4c. The multi-year averaged surface atmospheric pressure anomaly [hPa]
and the calculated quasi-geostrophic wind field [m/s] for selected months:
August
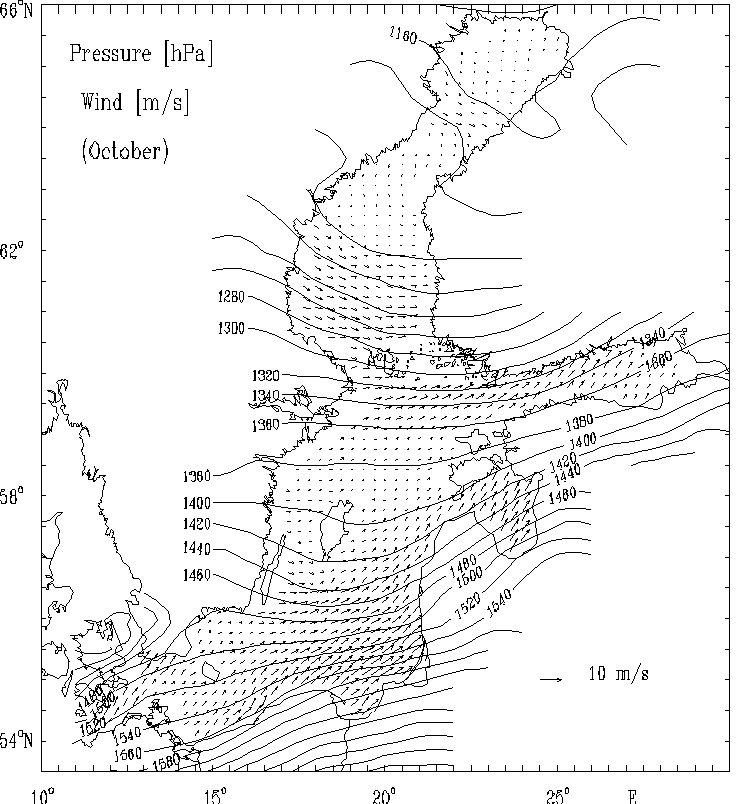
Figure 4d. The multi-year averaged surface atmospheric pressure anomaly [hPa]
and the calculated quasi-geostrophic wind field [m/s] for selected months:
October.
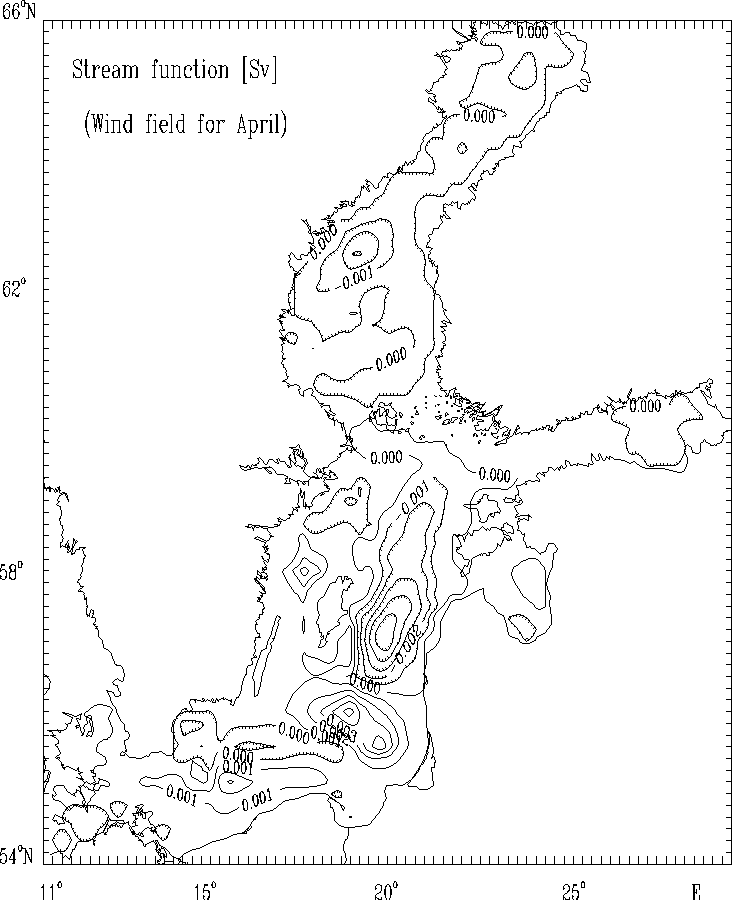
Figure 5a. Stream function for mass transport [Sv]
for selected months:
April. The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
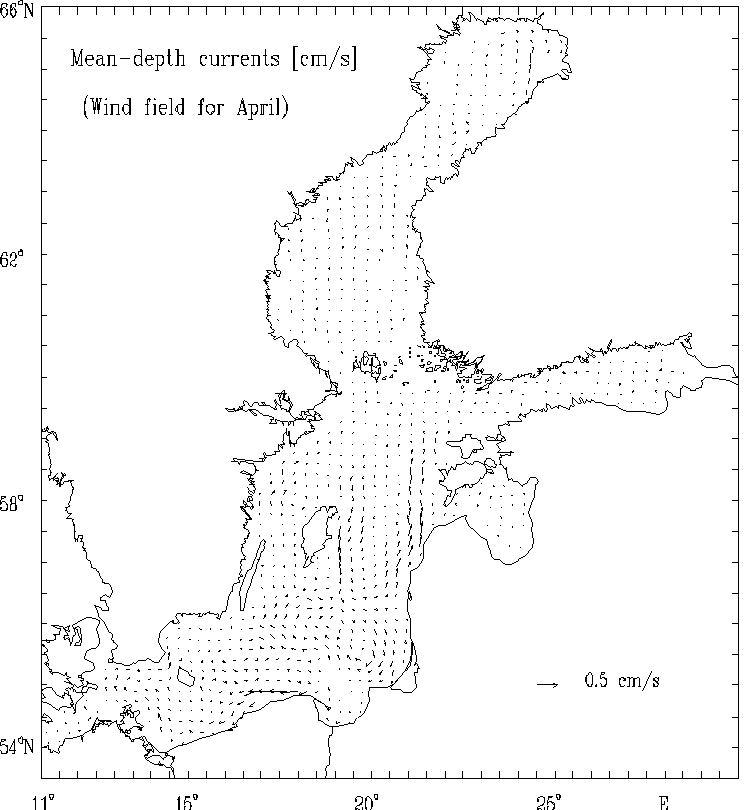
Figure 5b. Mean - depth currents [cm/s]
for selected months:
April.
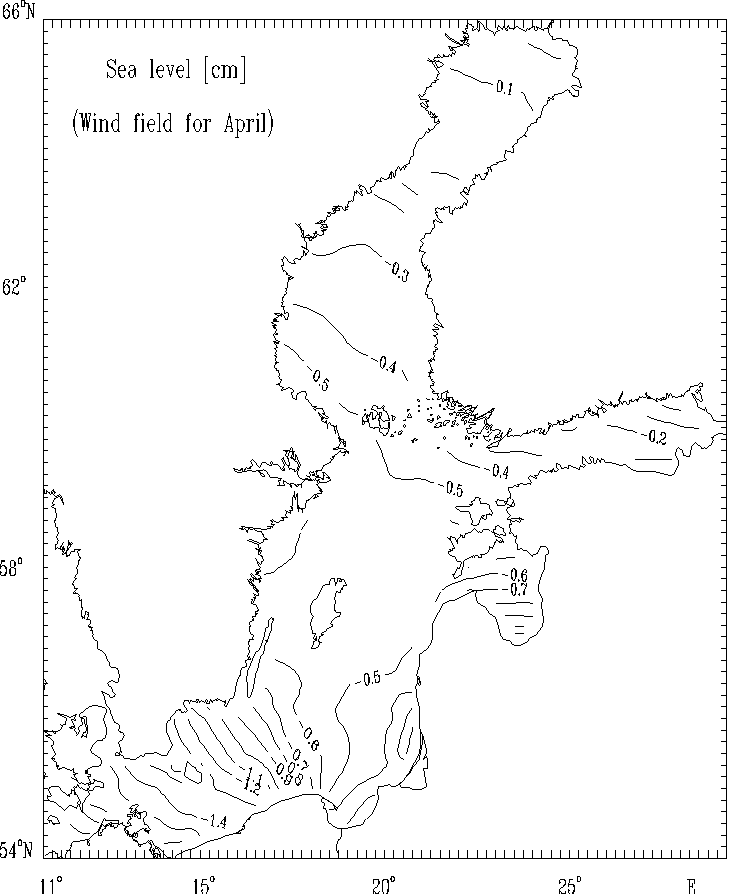
Figure 5c. Sea level [cm] for selected months:
April.
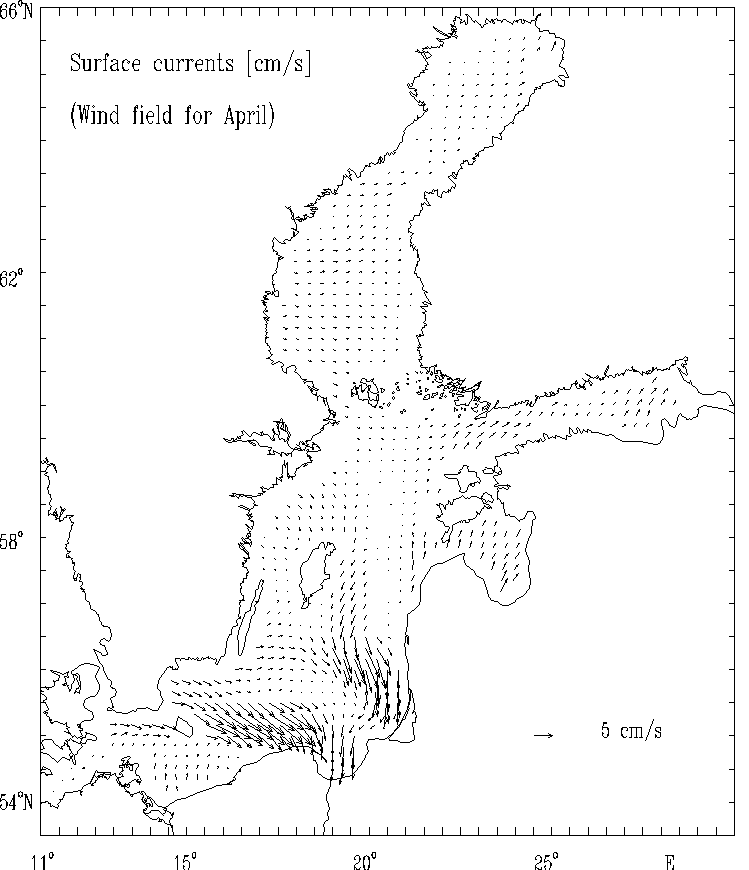
Figure 5d. Surface currents [cm/s] for selected months:
April.
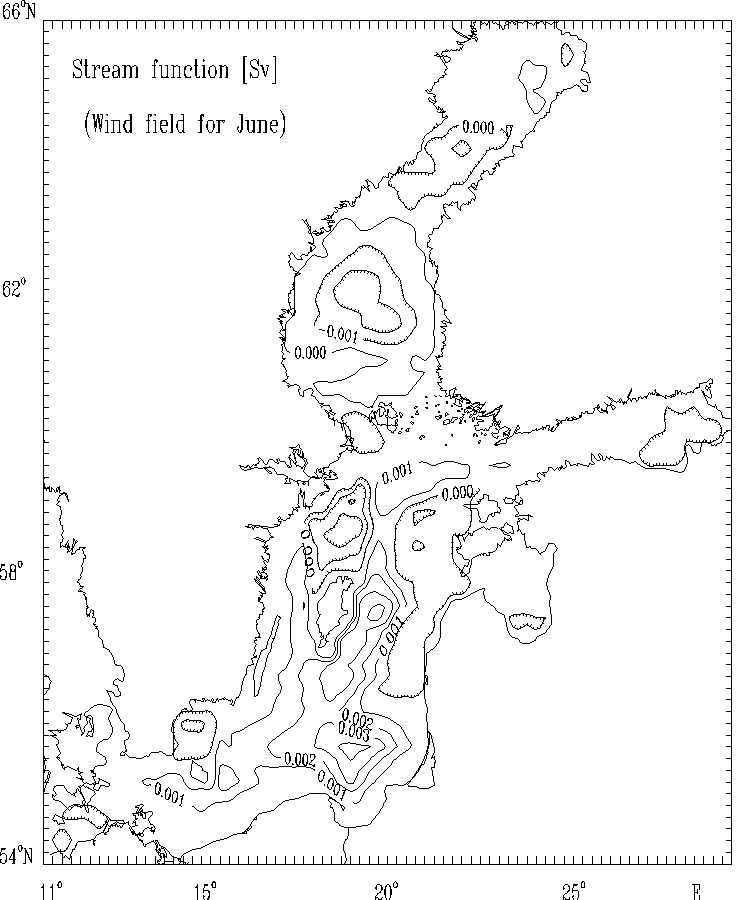
Figure 6a. Stream function for mass transport [Sv]
for selected months:
June. The hatched areas indicate the regions of counterclockwise (cyclonic) water circulation.
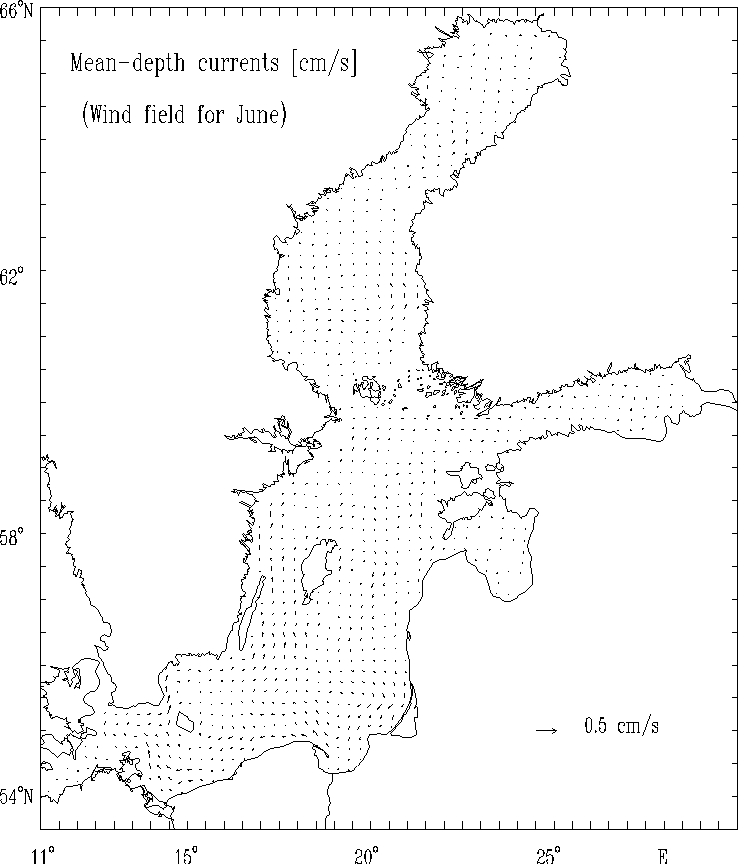
Figure 6b. Mean - depth currents [cm/s], for selected months: June.
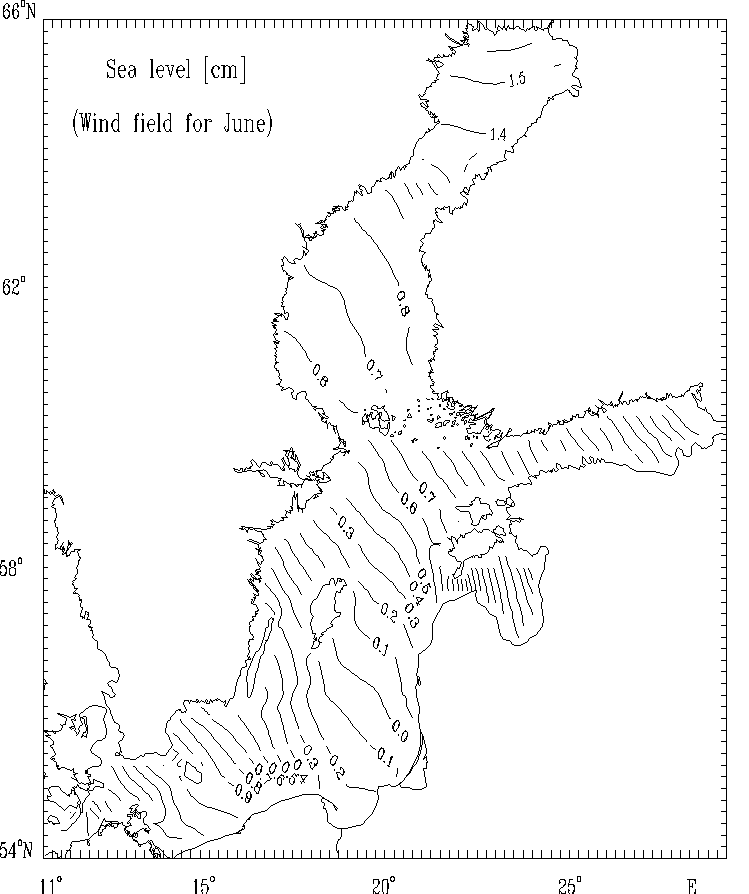
Figure 6c.
Sea level [cm] for selected months: June.
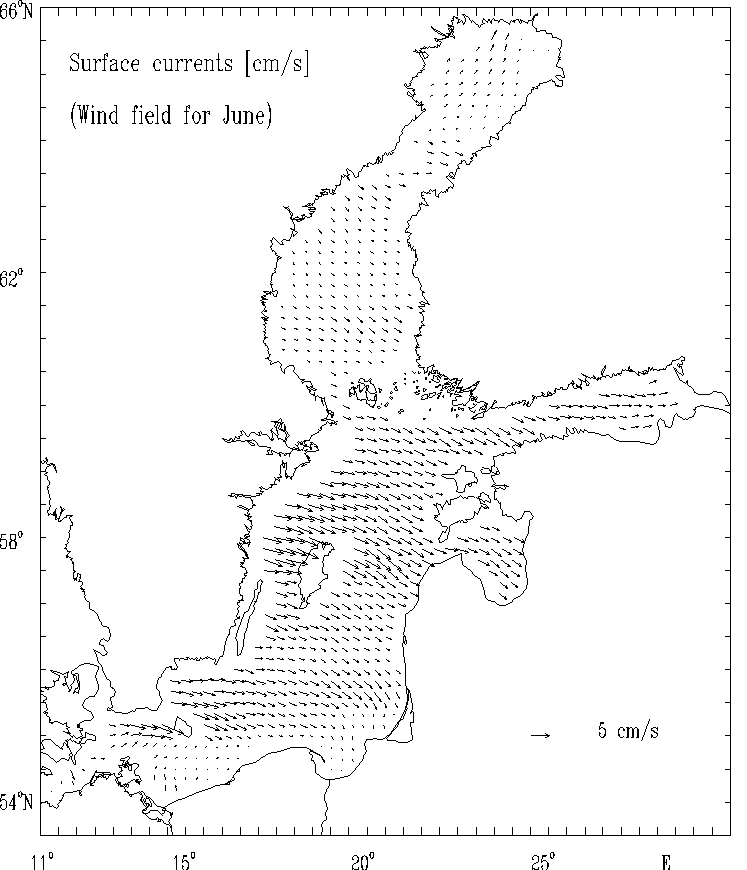
Figure 6d.
Surface currents [cm/s] for selected months:
June.
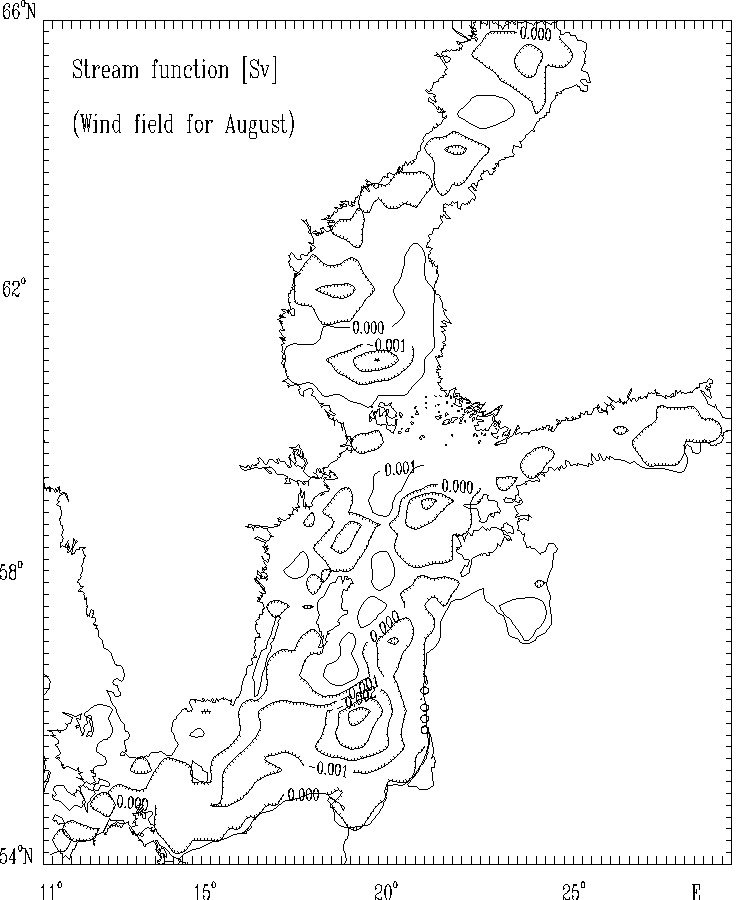
Figure 7a. Stream function for mass transport [Sv]
for selected months: August.
The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
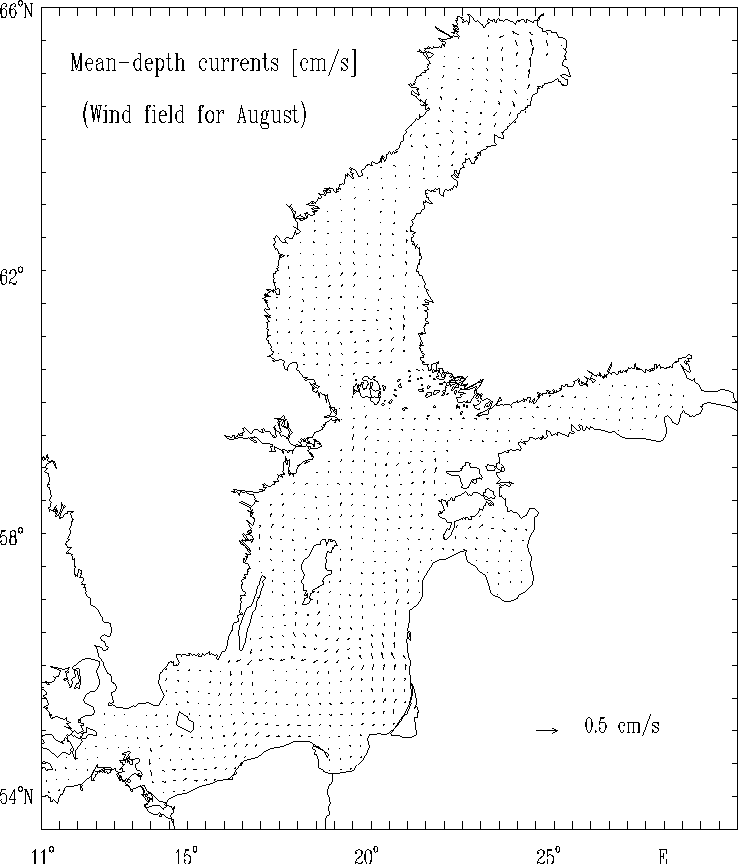
Figure 7b. Mean - depth currents [cm/s]
for selected months: August.
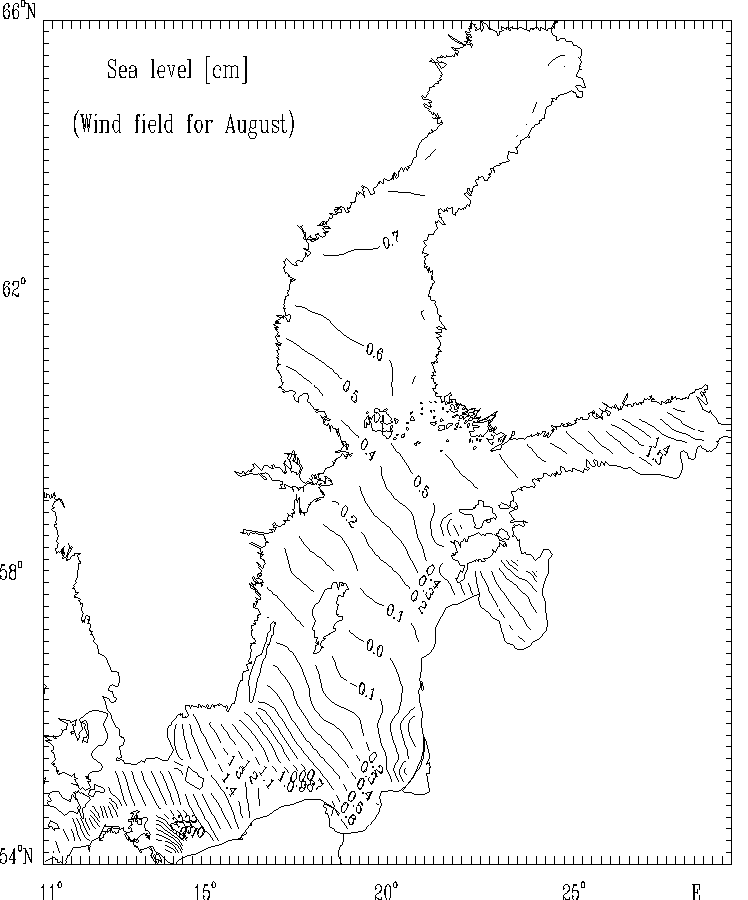
Figure 7c.
Sea level [cm] for selected months: August.
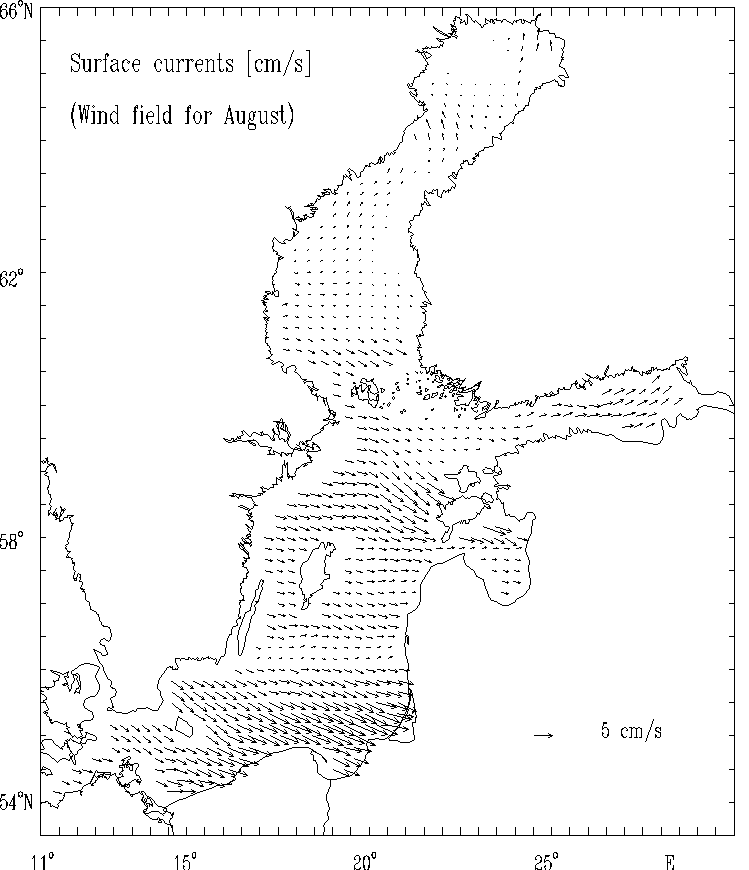
Figure 7d.
Surface currents [cm/s] for selected months:
August.
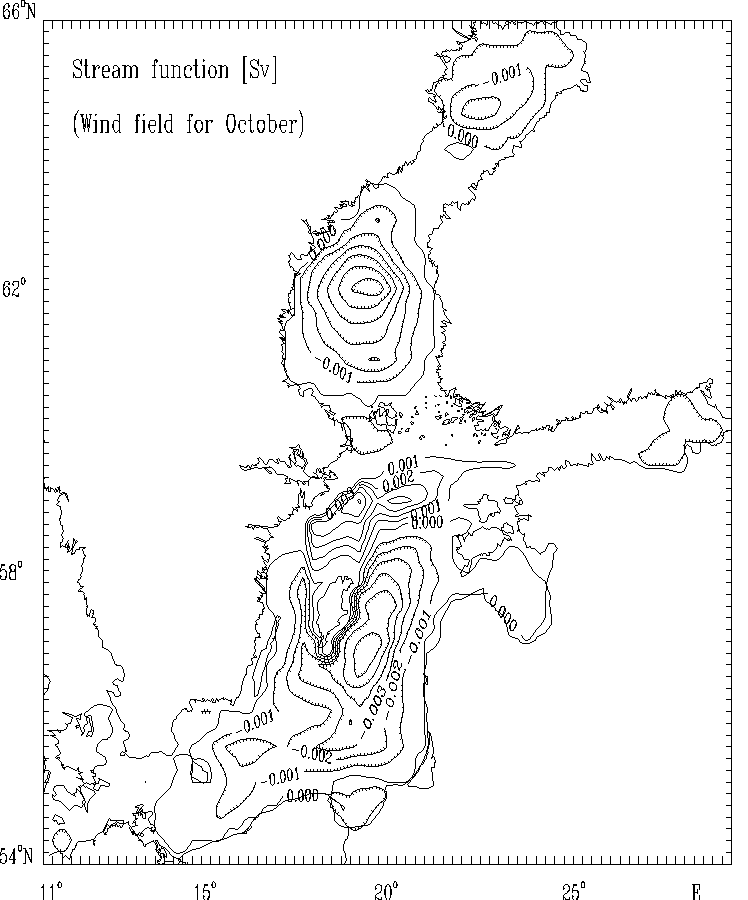
Figure 8a. Stream function for mass transport [Sv]
for selected months: October.
The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
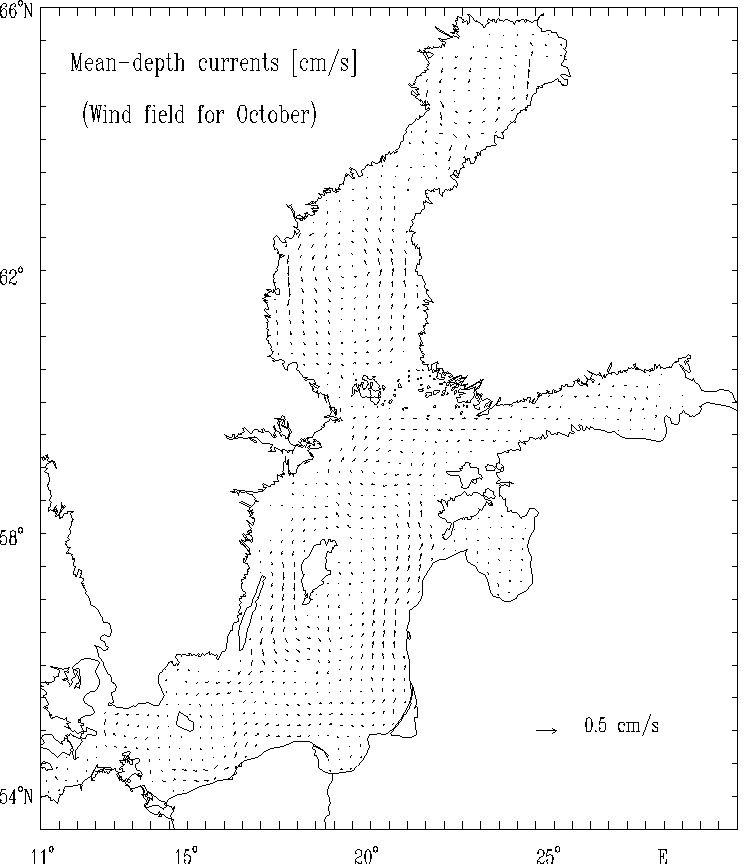
Figure 8b. Mean - depth currents [cm/s]
for selected months: October.
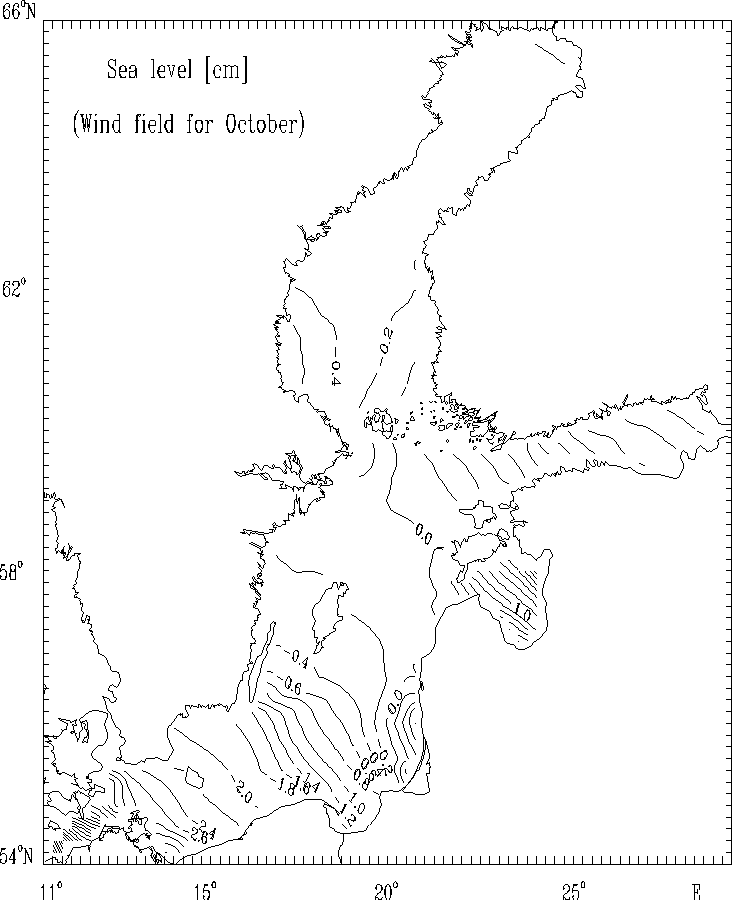
Figure 8c.
Sea level [cm] currents [cm/s] for selected months:
October.
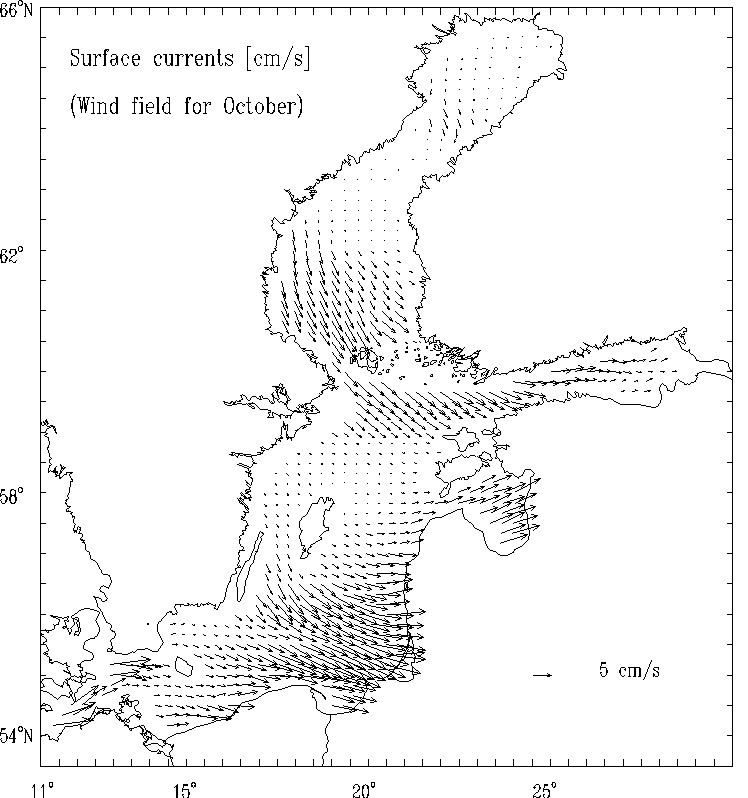
Figure 8d.
Surface currents [cm/s] for selected months:
October.
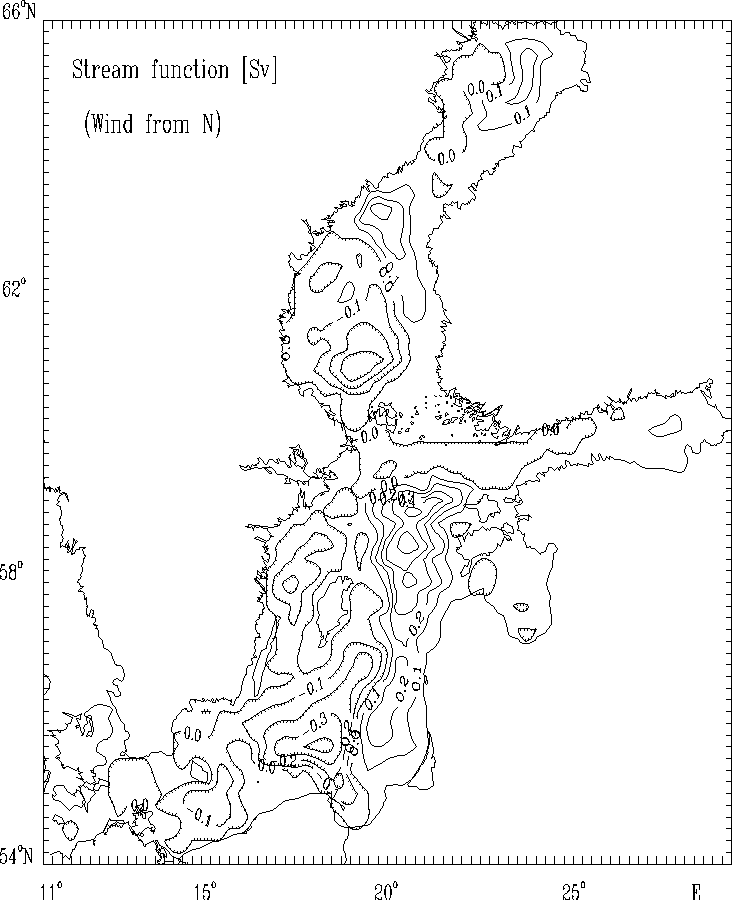
Figure 9a. Stream function for mass transport [Sv]
for the strong wind of constant velocity blowing from North.
The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
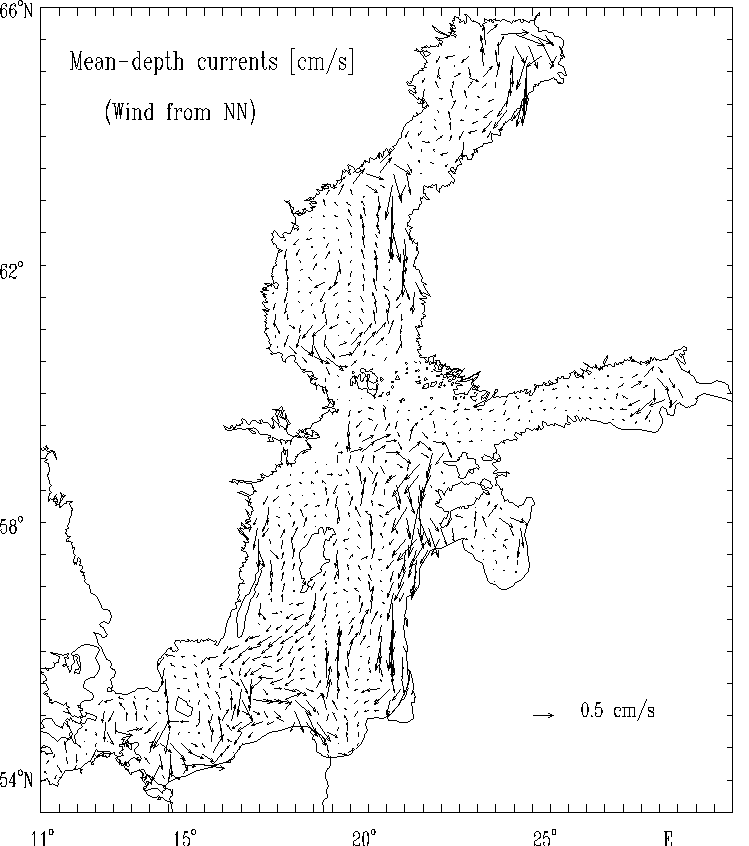
Figure 9b. Mean - depth currents [cm/s]
for the strong wind of constant velocity blowing from North.
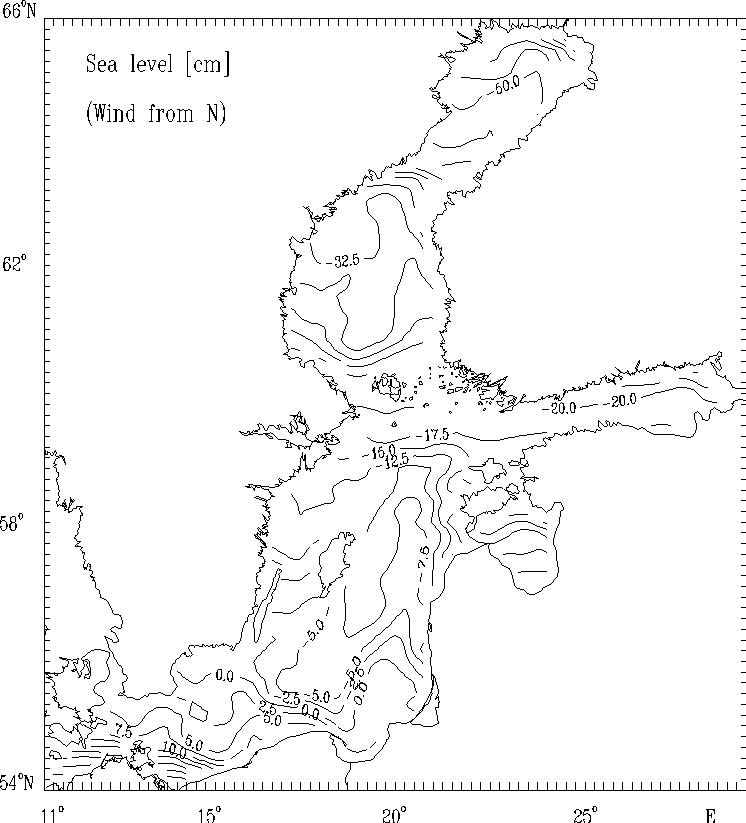
Figure 9c.
Sea level [cm] for the strong wind of constant
velocity blowing from North.
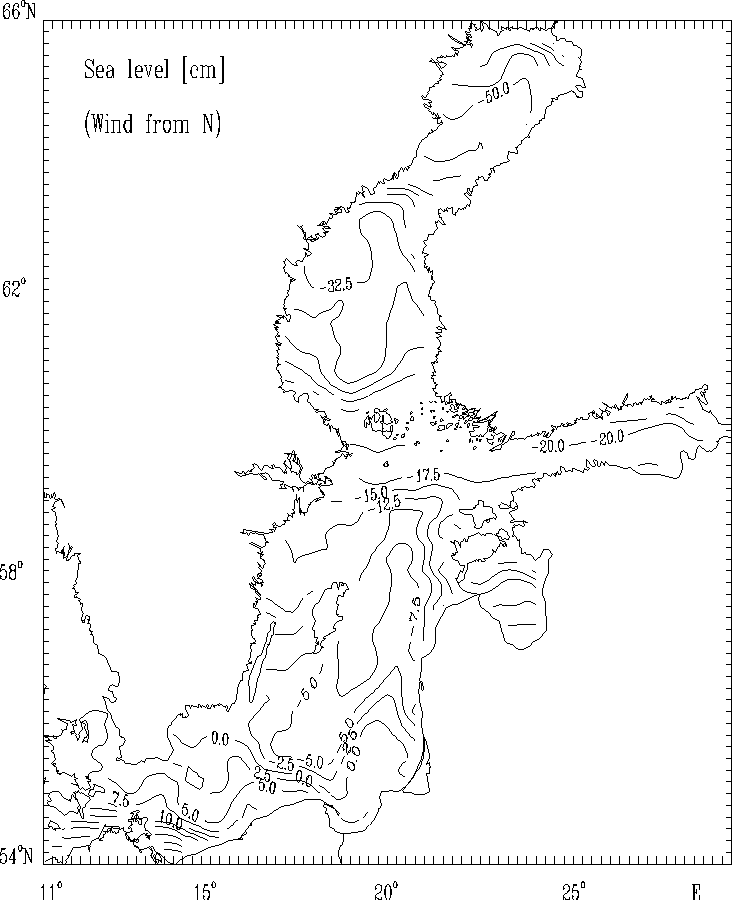
Figure 9d.
Surface currents [cm/s] for the strong wind of constant
velocity blowing from North.
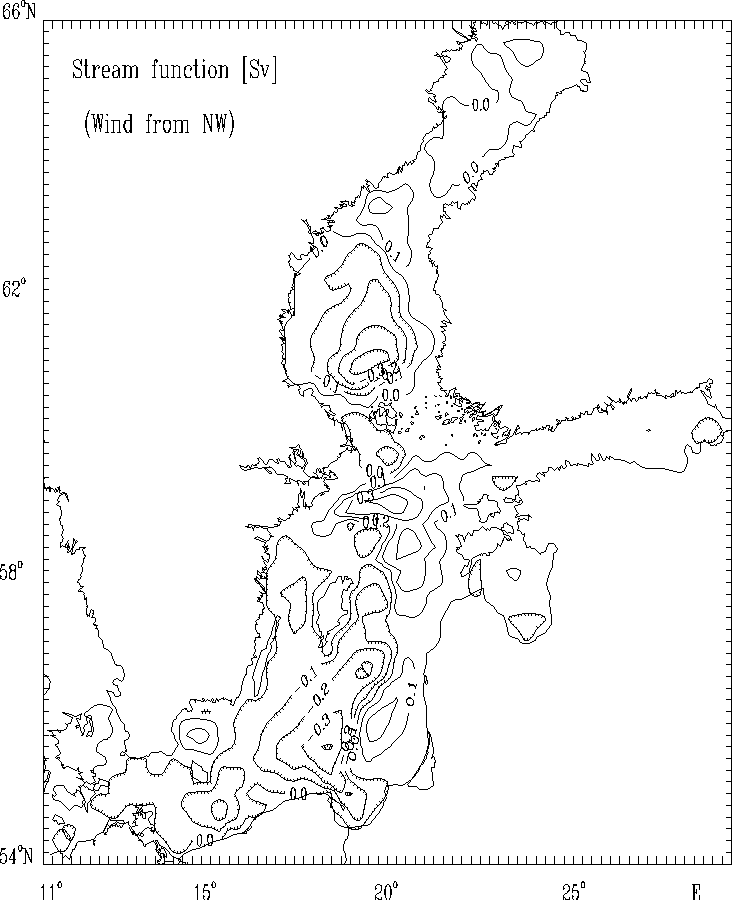
Figure 10a. Stream function for mass transport [Sv]
for the strong wind of constant
velocity blowing from Northwest.
The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
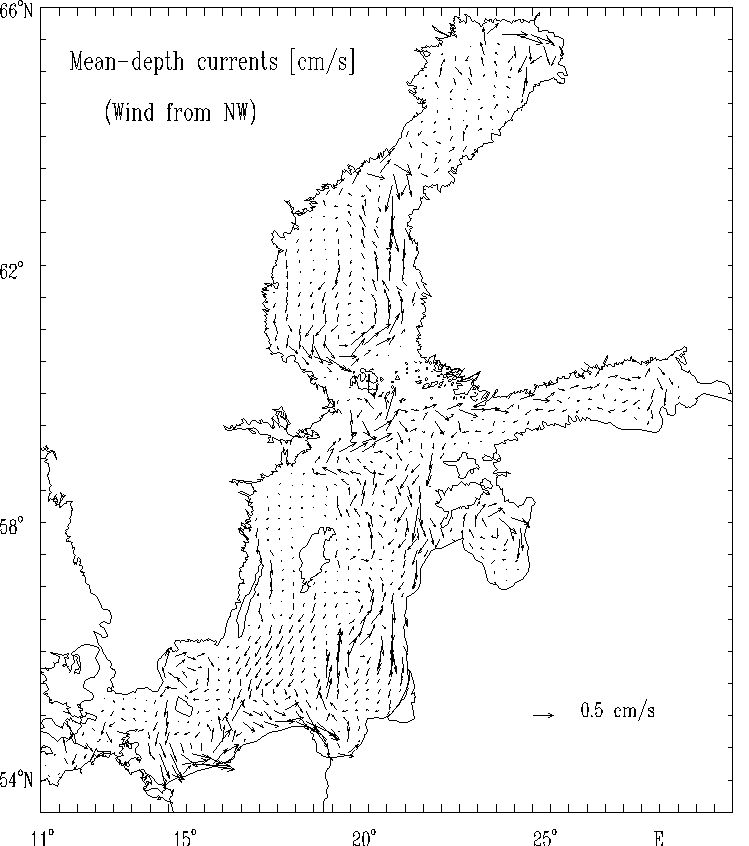
Figure 10b. Mean - depth currents [cm/s]
for the strong wind of constant
velocity blowing from Northwest.
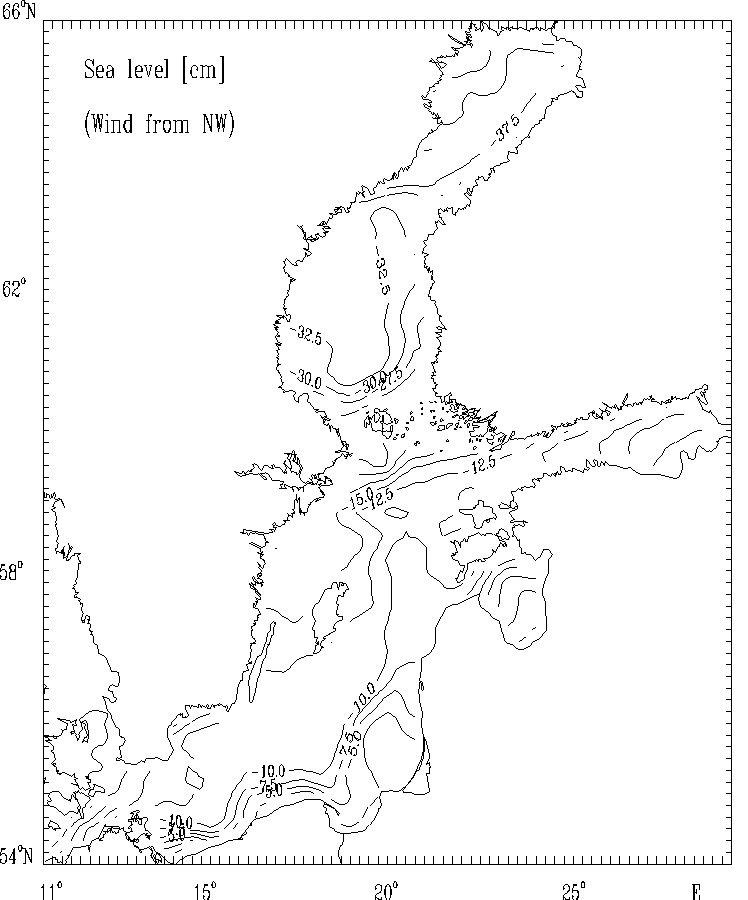
Figure 10c.
Sea level [cm] for the strong wind of constant
velocity blowing from Northwest.
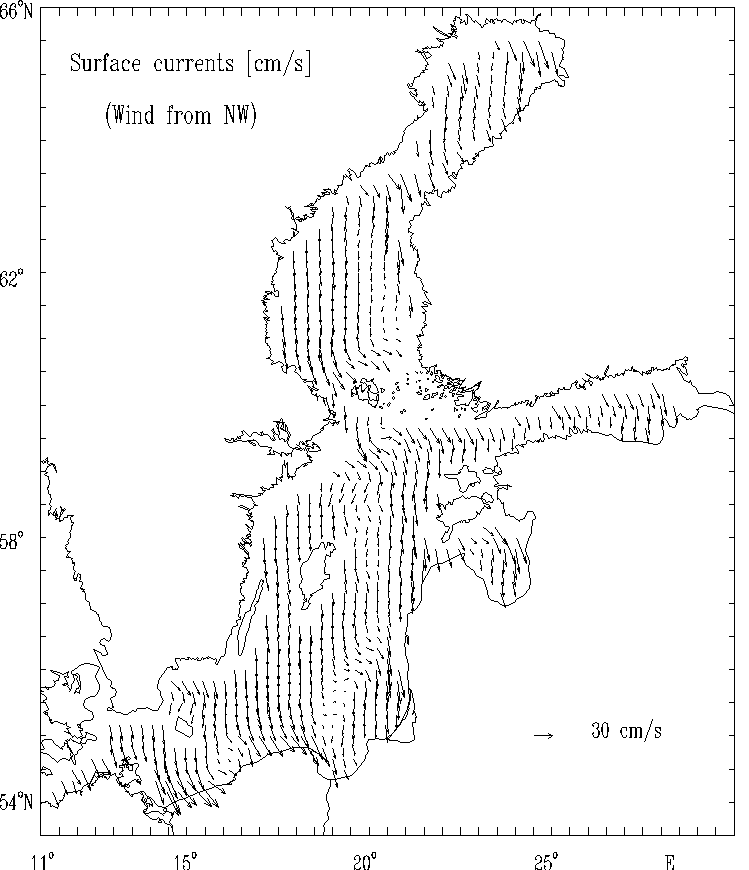
Figure 10d.
Surface currents [cm/s] for the strong wind of constant
velocity blowing from Northwest.
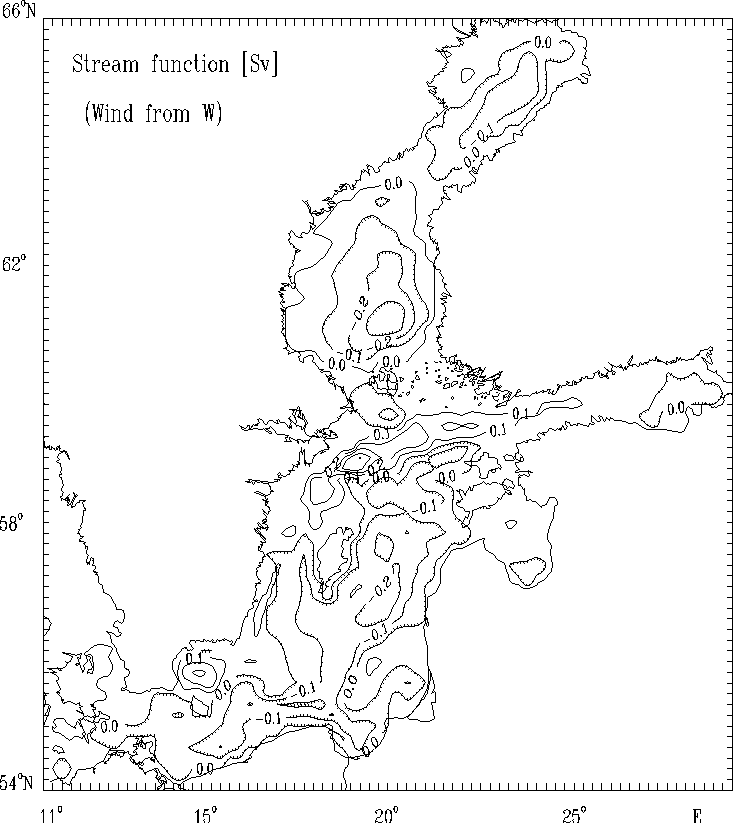
Figure 11a. Stream function for mass transport [Sv]
for the strong wind of constant
velocity blowing from West.
The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
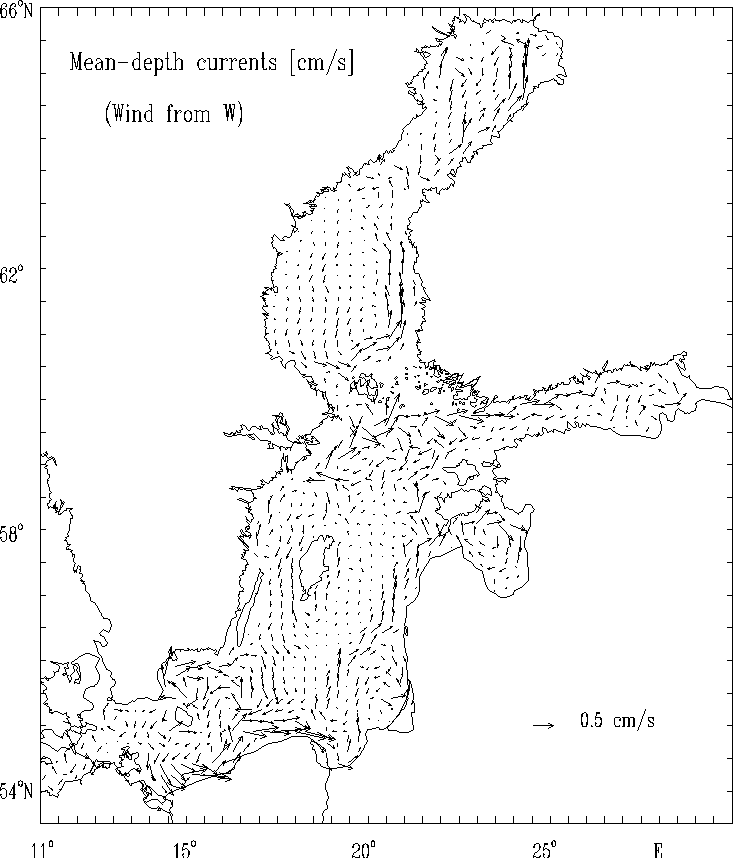
Figure 11b. Mean - depth currents [cm/s]
for the strong wind of constant
velocity blowing from West.
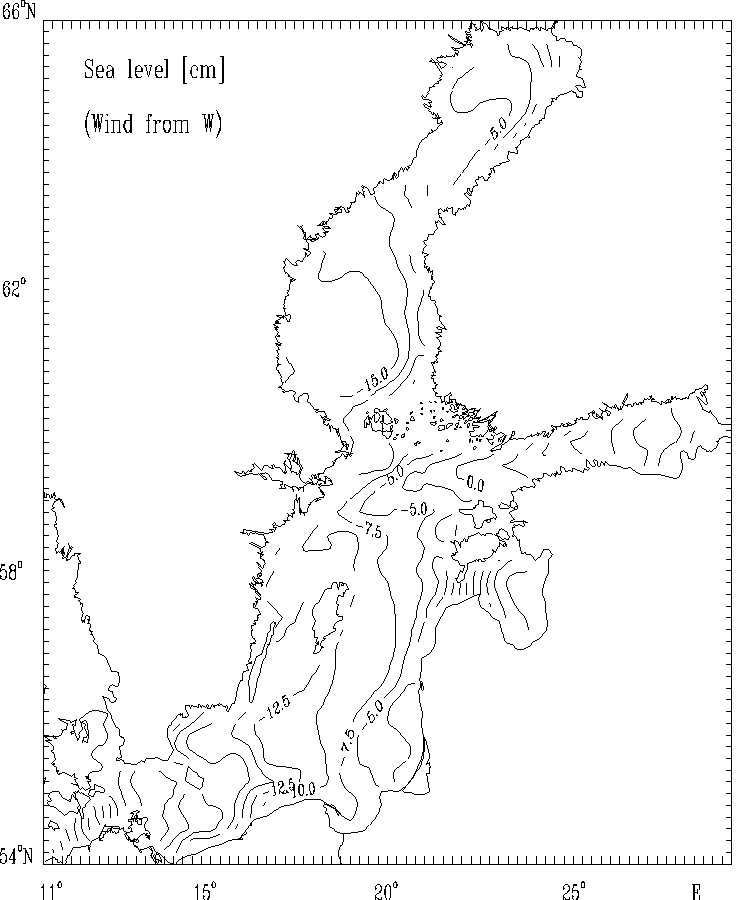
Figure 11c.
Sea level [cm] for the strong wind of constant
velocity blowing from West.
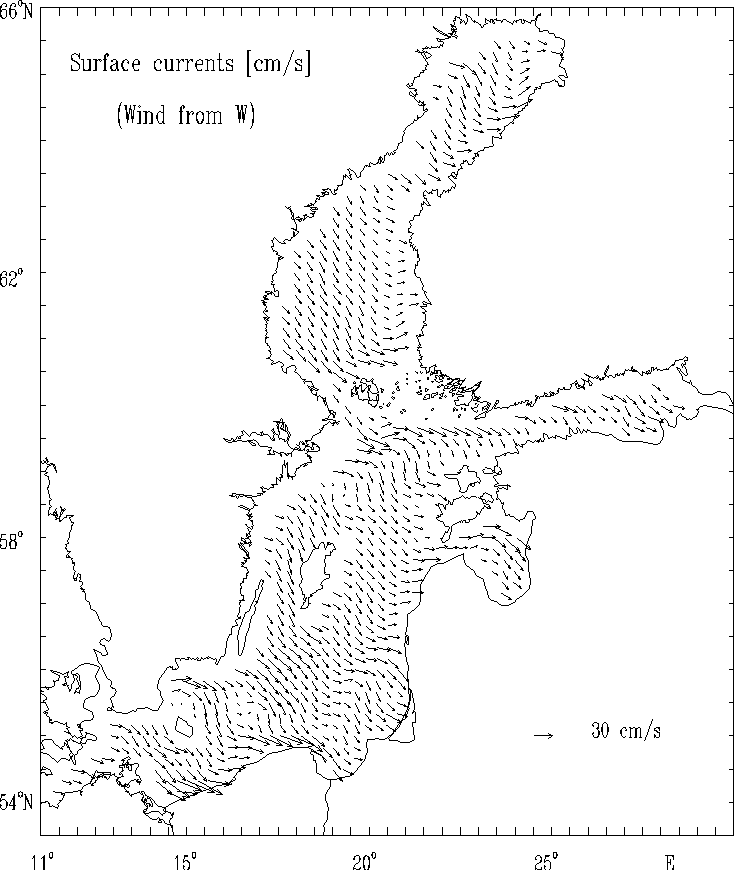
Figure 11d.
Surface currents [cm/s] for the strong wind of constant
velocity blowing from West.
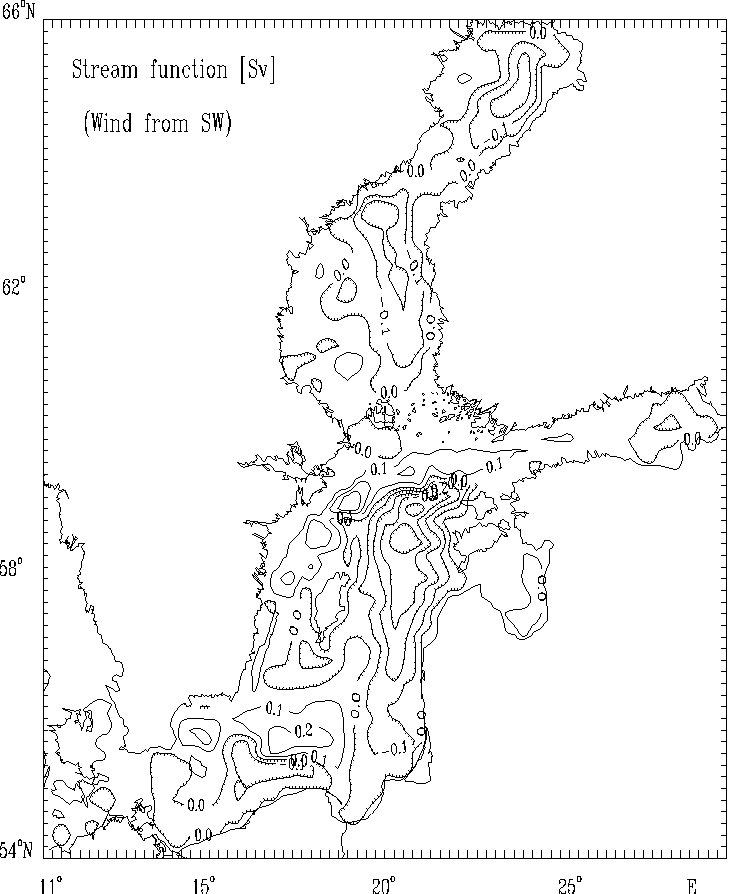
Figure 12a. Stream function for mass transport [Sv]
for the strong wind of constant
velocity blowing from Southwest.
The hatched areas indicate the regions
of counterclockwise (cyclonic) water circulation.
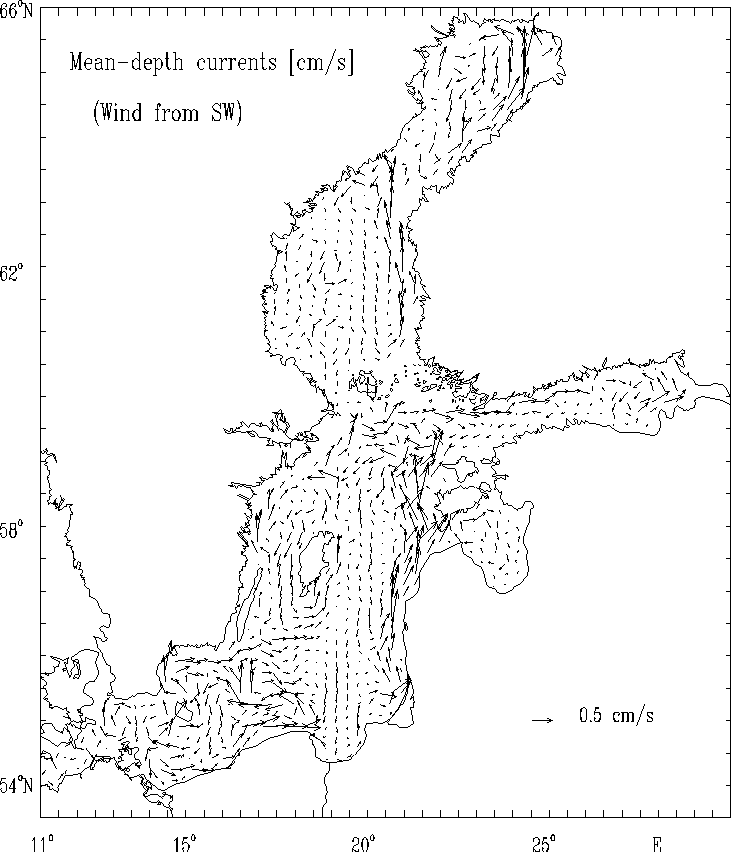
Figure 12b. Mean - depth currents [cm/s]
for the strong wind of constant
velocity blowing from Southwest.
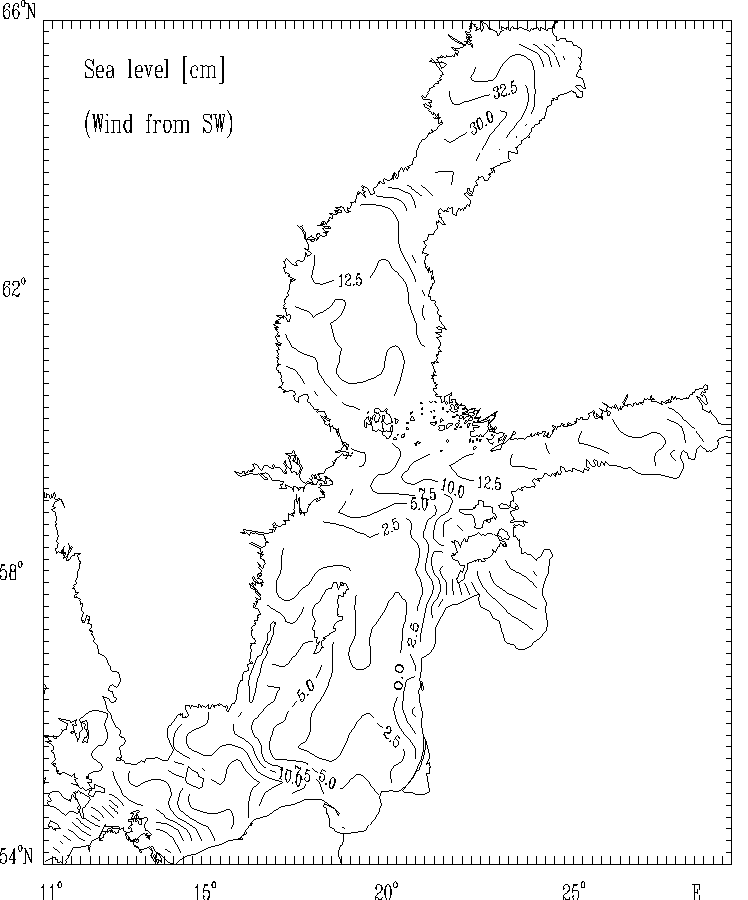
Figure 12c.
Sea level [cm] for the strong wind of constant
velocity blowing from Southwest.
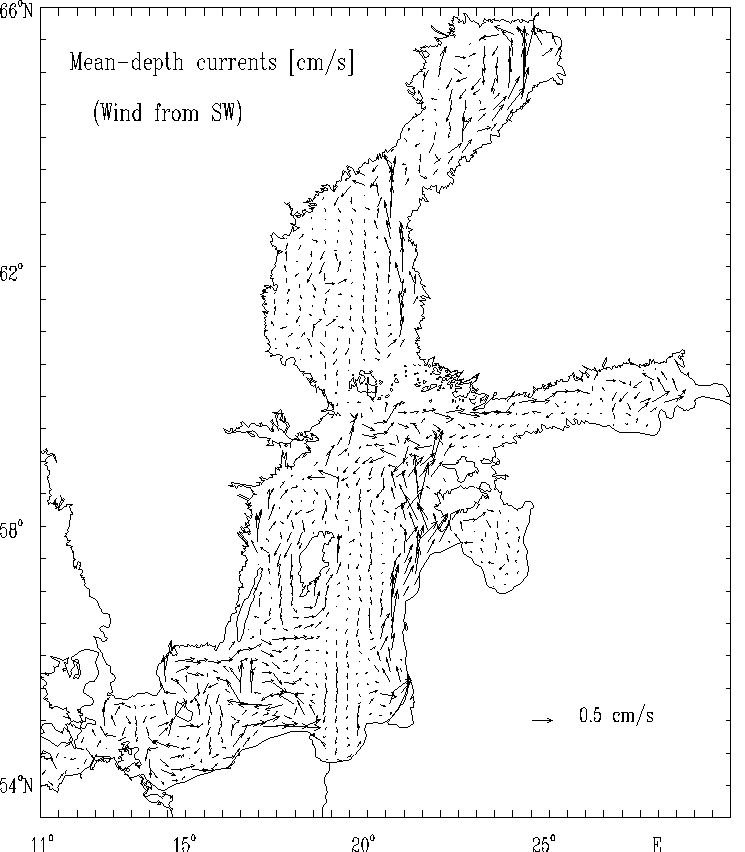
Figure 12d.
Surface currents [cm/s] for the strong wind of constant
velocity blowing from Southwest.